所有你需要知道的关于统计和概率的知识都在这里了

免费预览：

统计和概率：

统计和概率是当今世界最具革命性技术的基石。从人工智能到机器学习和计算机视觉，统计和概率构成了所有这些技术的基础。在这篇关于统计和概率的文章中，我打算帮助你理解最复杂的算法和技术背后的数学原理。

 

本文中涵盖了以下内容：

1. 什么是数据？
2. 数据类别
3. 什么是统计？
4. 统计学中的基本术语
5. 抽样技术
6. 统计类型
7. 描述性统计
   1. 中心测量
   2. 传播措施
   3. 信息增益和熵
   4. 混淆矩阵
8. 概率
   1. 什么是概率？
   2. 概率术语
   3. 概率分布
   4. 概率的类型
   5. 贝叶斯定理
9. 推论统计
   1. 点估计
   2. 区间估计
   3. 估计置信水平
   4. 假设检验

什么是数据？

环顾四周，到处都是数据。每次点击手机都会产生比您知道的更多的数据。这些生成的数据为分析提供了洞察力，并帮助我们做出更好的业务决策。这就是数据如此重要的原因。

什么是数据 – 统计和概率 

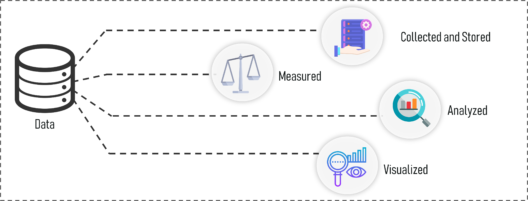
数据是指事实或收集的统计数据汇总成为参考或分析的原材料。 

可以收集、测量和分析数据，也可以通过使用统计模型和图表来可视化。

数据类别

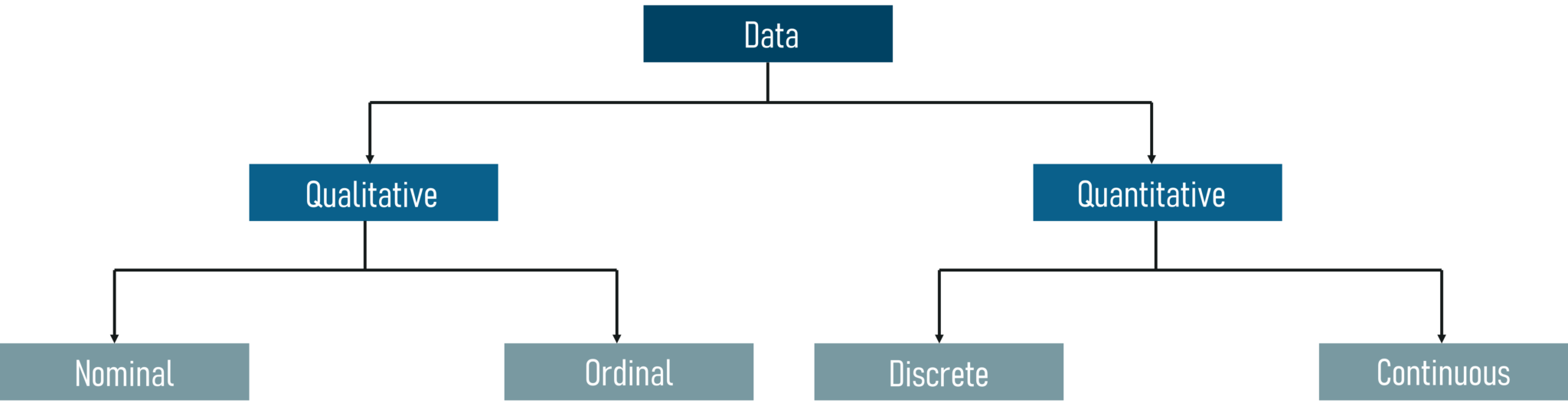
数据可以分为两个子类别：

1. 定性数据
2. 定量数据

请参考下图了解不同类别的数据：

数据类别 – 统计和概率 

定性数据： 定性数据处理的特征和描述符不易测量，但可以主观观察。定性数据进一步分为两类数据：

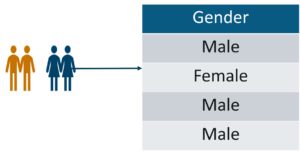
• 名义数据：没有固有顺序或排名的数据，例如性别或种族。

名义数据 – 统计和概率

• 序数数据：具有有序信息序列的数据称为序数数据。

序数数据 – 统计和概率 

定量数据： 定量数据可以处理客观衡量的数字和事物。这又分为两种：

• 离散数据：也称为分类数据，它可以保存有限数量的可能值。

示例：一个班级的学生人数。

• 连续数据：可以保存无限数量的可能值的数据。

示例：一个人的重量。

接下来的部分将重点介绍基本的统计概念，因此准备好回顾一些数学运算。

什么是统计？

统计学是应用数学的一个领域，涉及数据收集、分析、解释和呈现。

什么是统计 - 统计和概率

这个数学领域涉及如何使用数据来解决复杂的问题。以下是使用统计数据解决几个问题的示例：

• 某公司开发了一种可以治愈癌症的新药。你将如何进行测试以确认药物的有效性？
• 你和一个朋友正在参加一场棒球比赛，他出人意料地向你打赌，两支球队都不会在那场比赛中击出全垒打。你应该下注吗？
• 最新的销售数据刚刚出来，你的老板要你为管理层准备一份关于公司可以改进业务的地方的报告。你应该找什么？不应该寻找什么？

使用统计技术可以很容易地解决上述这些问题。在接下来的部分中，我们将看到如何做到这一点。

统计学中的基本术语

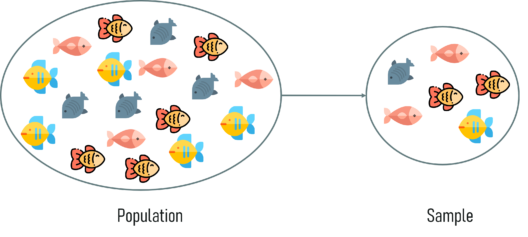
在深入了解统计学之前，了解统计学中使用的基本术语非常重要。统计学中最重要的两个术语是总体和样本。

人口和样本 - 统计和概率 

• 总体：要分析其属性的个体或对象或事件的集合
• 样本：总体的一个子集称为“样本”。精心挑选的样本将包含有关特定对象的大部分信息范围。

现在您一定想知道如何选择最能代表整个总体的样本。

抽样技术

抽样是一种统计方法，用于处理总体中单个观测值的选择。用它来推断有关总体的统计知识。

考虑一个场景，您被要求对美国青少年的饮食习惯进行一项调查。目前美国有超过 4200 万青少年，并且随着您阅读此博客，这个数字还在增长。是否有可能对这 4200 万人中的每一个人进行调查以了解他们的健康状况？显然不是！这就是使用抽样的原因。这是一种方法，其中研究人口样本以得出关于整个人口的推论。

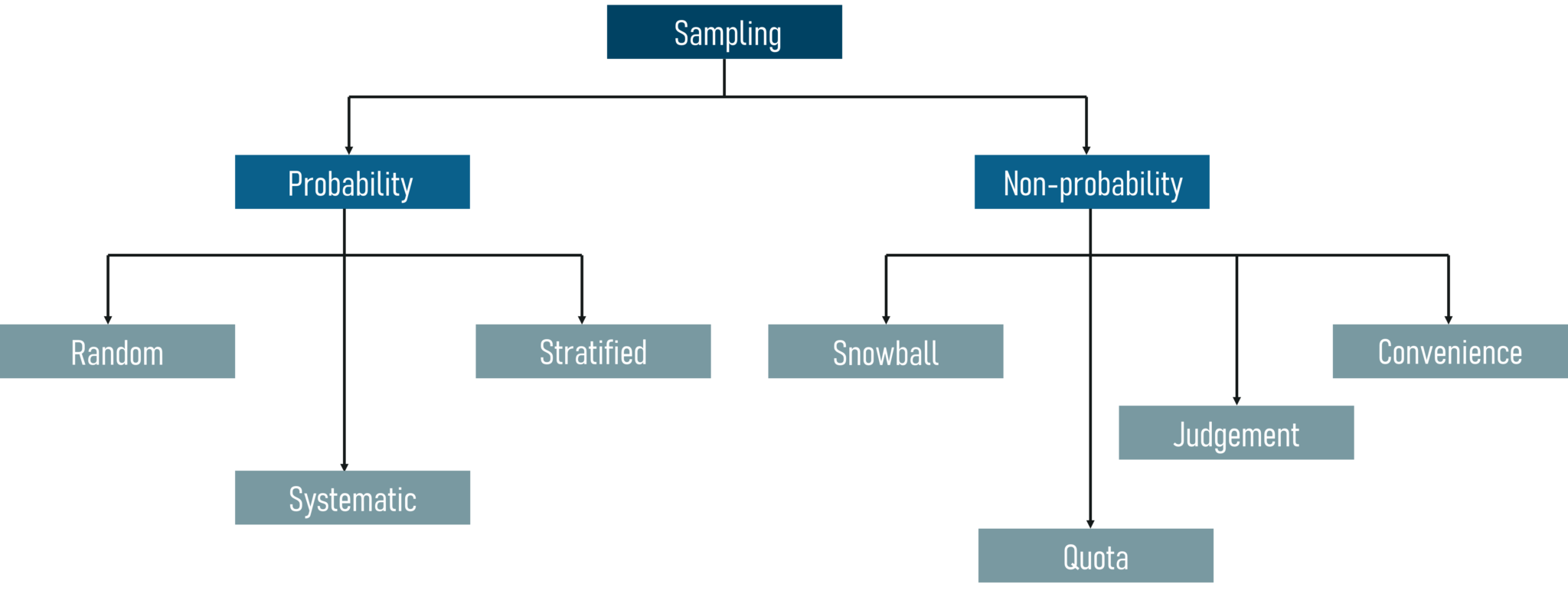
采样技术主要有两种类型：

1. 概率抽样
2. 非概率抽样

抽样技术 – 统计和概率 

在本文中，我们将只关注概率抽样技术，因为非概率抽样不在本文的范围内。

概率抽样：这是一种抽样技术，其中使用概率理论从大量人口中选择样本。概率抽样的三种类型：

• 随机抽样：在这种方法中，总体中的每个成员在样本中被选中的机会均等。

随机抽样 – 统计和概率 

• 系统抽样：在系统抽样中，从总体中选择每第 n 个记录作为样本的一部分。请参阅下图以更好地了解系统抽样的工作原理。

系统抽样 – 统计和概率 

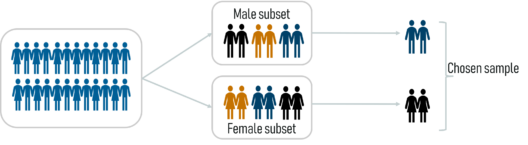
• 分层抽样：在分层抽样中，一个层用于从大量人口中形成样本。阶层是具有至少一个共同特征的人口子集。在此之后，使用随机抽样的方法从每个层中选择足够数量的受试者。

分层抽样 – 统计和概率

现在你知道了统计的基础知识，让我们继续讨论不同类型的统计。

统计类型

那里有两个定义明确的统计类型：

1. 描述性统计
2. 推论统计

描述性统计

描述性统计是一种通过给出关于样本和数据度量的简短摘要来描述和理解特定数据集特征的方法。

描述性统计主要关注数据的主要特征。它提供了数据的图形摘要。

描述性统计 - 统计和概率

假设您想赠送所有同学的 T 恤。要研究教室中学生的平均衬衫尺码，在描述性统计中，您将记录班上所有学生的衬衫尺码，然后您将找出班级的最大、最小和平均衬衫尺码。

推论统计

推论统计基于从相关人口中获取的数据样本对人口进行推断和预测。

推论统计概括了一个大型数据集并应用概率得出结论。它允许我们使用样本数据基于统计模型推断数据参数。

推论统计 - 统计和概率

因此，与我们考虑在一个班级中求出学生的平均衬衫尺寸的示例相同，在推理统计中，您将抽取班级的样本集，基本上是全班的几个人。您已经将衬衫尺寸分为大、中、小。在这种方法中，您基本上构建了一个统计模型并将其扩展到整个班级中。

以上就是对描述统计和推论统计的简要了解。在接下来的部分中，您将看到描述性和推理性统计工作深入。

了解描述性统计

描述性统计分为两类：

1. 集中趋势测度
2. 变异性测量（散布）

中心测量 

中心度量是代表数据集摘要的统计度量。中心的三个主要措施：

中心度量 – 统计和概率 

1. 平均值：样本中所有值的平均值的度量称为平均值。
2. 中值：样本集中心值的度量称为中值。
3. 众数：样本集中出现频率最高的值称为众数。

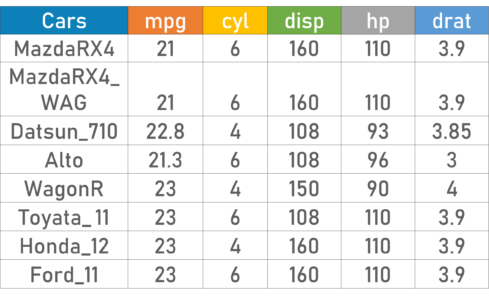
为了更好地理解集中趋势的度量，让我们看一个例子。以下汽车数据集包含以下变量：

数据集 – 统计和概率

• 汽车
• 每加仑里程数（mpg）
• 气缸类型 (cyl)
• 位移（disp）
• 马力(hp)
• 实际轴比(drat)

使用描述性分析，您可以分析样本数据集中每个变量的平均值、标准差、最小值和最大值。

如果我们想找出所有汽车中汽车的平均马力或平均马力，我们将检查并计算所有值的平均值。在这种情况下，我们将每辆车的马力总和除以汽车总数：
平均值 = (110+110+93+96+90+110+110+110)/8 = 103.625

如果我们想在汽车人口中找出mpg的中心值，我们将mpg值按升序或降序排列，并选择中间值。在这种情况下，我们有 8 个值，这是一个偶数条目。因此，我们必须取两个中间值的平均值。
8辆车的mpg：21,21,21.3,22.8,23,23,23,23
Median = (22.8+23 )/2 = 22.9

如果我们想找出汽车中最常见的气缸类型，我们将检查重复次数最多的值。在这里我们可以看到圆柱体有两个值，4 和 6。看一下数据集，您可以看到最经常出现的值是 6。因此 6 是我们的模式。

传播的措施

扫码免登录支付

本文章为付费文章，是否支付1宇宙币后完整阅读？

如果您已购买过该文章，[登录帐号]后即可查看

支付1宇宙币